Question
Write public and private key where p = 13, q = 37 and n = 481....
Write public and private key where p = 13, q = 37 and n = 481. Totient is 432. E is 19 and d is 91. Write public key as (n = , e =) and private key as (n = , d =)
Homework Answers
Answer #1
We proceed step by step, to verify all given information.
- p = 13, q = 37
- Thus, totient function
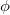 (n) = (p - 1) * (q - 1) = 12 * 36 = 432
(n) = (p - 1) * (q - 1) = 12 * 36 = 432
- Thus, totient function is as expected.
- We need to chose e < n, so that GCD (e, n) = 1
- e = 19 and n = 481 are relatively coprime, as GCD (19, 481) = 1. So, value of e is as expected.
- Also, d should be chosen, so that when (e * d) is divided by
totient function, the remainder is 1.
- e * d = 19 * 91 = 1729
- Also, 1729 = 1728 + 1 = (432 * 4) + 1 =
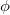 (n) + 1
(n) + 1 - So, d is also fine.
Thus, the keys are
- public key = (n, e) = (481, 19)
- private key = (n, d) = (481, 91)
Not the answer you're looking for?
Similar Questions
p = 13 q = 37 Totient = 432 n = 481 e = 19 d...
p = 13
q = 37
Totient = 432
n = 481
e = 19
d = 91
public key: n = 481, e = 19
private key: n= 481, d = 91
Except 1, explain any other prime number less than e which
cannot be used to generate d? What are those number and why they
cannot be used?
Discrete Math: decipher the following: 392466 600311 599633 where the public key is (950141,11), 950141=p*q 11=e...
Discrete Math:
decipher the following:
392466 600311 599633
where the public key is (950141,11), 950141=p*q 11=e
and the private key (d) is 603395
Let p=11, q=17, n = pq = 187. Your (awful) public RSA encryption key is (e=107,...
Let p=11, q=17, n = pq = 187. Your (awful) public RSA encryption
key is (e=107, n=187). (a) What is your private decryption key? (b)
You receive the encrypted message: 100 Decrypt the message. (In
other words, what was the original message, before it was
encrypted? Just give me a number, don’t convert it to letters).
Q1: Sara is using RSA crypto-system with the following setup: p = 11 and q =...
Q1: Sara is using RSA
crypto-system with the following setup: p = 11 and
q = 3. Sara publish his Public Key: (n, e)
= (33, 3).
d. Deem wants to set up his own public and private keys. She
chooses p = 23 and q = 19 with e = 283. Find her private and public
keys. Note show all steps to find the good value for d.
RSA Cryptography Perform encryption and decryption to find private decryption key d. a. p = 3,...
RSA Cryptography
Perform encryption and decryption to find private decryption key
d.
a. p = 3, q = 13, e = 7
b. p = 787, q = 631, e = 234559
Suppose the totient for a given public key (52,494,503;7) is inadvertently released and is equal to...
Suppose the totient for a given public key (52,494,503;7) is
inadvertently released and is equal to 52,479,768. What are p and
q? What is the decryption exponent d? For extra credit what is the
plaintext message of the ciphertext C=15,114,578 encrypted with the
given public key?
Suppose your RSA Public-key factors are p =6323 and q = 2833, and the public exponent...
Suppose your RSA Public-key factors are p =6323 and q = 2833,
and the public exponent e is 31. Suppose you were sent the
Ciphertext 6627708. Write a program that takes the above parameters
as input and implements the RSA decryption function to recover the
plaintext.
IN PYTHON
Below is an example of key generation, encryption, and decryption using RSA. For the examples below,...
Below is an example of key generation, encryption, and
decryption using RSA. For the examples below, fill in the
blanks to indicate what each part is or answer the
question.
Public key is (23, 11) What is 23 called?
_______________, What is 11 called?_______________
Private key is (23, 13) What is 23
called?_______________, What is 13
called?_______________
23 can be part of the public key because it is very hard
to _______________ large prime numbers.
ENCRYPT (m) = m^e mod...
Samantha uses the RSA signature scheme with primes p = 13 and q = 23 and...
Samantha uses the RSA signature scheme with primes p = 13 and q
= 23 and public verification exponent v = 53. (a) What is
Samantha’s public modulus? What is her private signing key? (b)
Samantha signs the digital document D = 100. What is the
signature?
For solving the problems, you are required to use the following formalization of the RSA public-key...
For solving the problems, you are required to use the following
formalization of the RSA public-key cryptosystem.
In the RSA public-key cryptosystem,
each participants creates his public key and secret key according
to the following steps:
· Select two very large
prime number p and q. The number of bits needed to represent p and
q might be 1024.
· Compute
n = pq
(n) = (p – 1) (q – 1).
The formula for (n) is owing to...
ADVERTISEMENT
Need Online Homework Help?
Get Answers For Free
Most questions answered within 1 hours.
ADVERTISEMENT
Active Questions
asked 7 minutes ago
asked 19 minutes ago
asked 20 minutes ago
asked 45 minutes ago
asked 45 minutes ago
asked 52 minutes ago
asked 52 minutes ago
asked 57 minutes ago
asked 1 hour ago
asked 1 hour ago
asked 1 hour ago
asked 1 hour ago
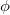 (n) = (p - 1) * (q - 1) = 12 * 36 = 432
(n) = (p - 1) * (q - 1) = 12 * 36 = 432