Let swap_every_two be an operation on languages that is defined as follows: swap_every_two(L) = {a2a1a4a3 ....
Let swap_every_two be an operation on languages that is defined as follows:
swap_every_two(L) = {a2a1a4a3 . . . a2na2n−1 | a1a2a3a4 . . . a2n−1a2n ∈ L where a1, . . . , a2n ∈ Σ} In this definition, Σ is the alphabet for the language L.
1. What languages result from applying swap every two to the following languages:
(a) {1 n | n ≥ 0}, where the alphabet is {1}.
(b) {(01)n | n ≥ 0}, where the alphabet is {0, 1}.
2. Show that if L is a regular language then so it swap every two(L).
below is a hint Hint: Try to construct an automaton accepting swap every two(L) from a DFA accepting L. The automaton you construct should conceptually process the input symbols in pairs, using its finite control to somehow remember the first symbol of the pair. If you use such a “proof-by-construction” approach, you should define the automaton formally and provide a brief, informal argument to show that your automaton accepts swap every two(L).
plz provide full detail! this assignment is very important for me
Homework Answers
1 (a) The language given is  , and the operation swap_every_two is to be applied to L.
According to the definition of the operation
swap_every_two, for every string
, and the operation swap_every_two is to be applied to L.
According to the definition of the operation
swap_every_two, for every string  , swap_every_two(L) should contain the strings
, swap_every_two(L) should contain the strings  . So, this would mean that swap_every_two(L) should be
formed by swapping the alternate symbols of all strings of even
length in L. However, for the given language, swapping the
alternate symbols should result in the same string. Thus, it would
contain all the even length strings in L, which can be written
as:
. So, this would mean that swap_every_two(L) should be
formed by swapping the alternate symbols of all strings of even
length in L. However, for the given language, swapping the
alternate symbols should result in the same string. Thus, it would
contain all the even length strings in L, which can be written
as:

(b) The language given is  . On applying the operation swap_every_two to L, the
strings obtained by swapping alternate symbols of each member of L
should be returned. So, each
. On applying the operation swap_every_two to L, the
strings obtained by swapping alternate symbols of each member of L
should be returned. So, each  must be replaced with a
must be replaced with a  . Hence, the language returned by the operation is:
. Hence, the language returned by the operation is:

2. The following is a procedure to construct a N.F.A. for the language swap_every_two(L) where L is a regular language:
- Construct the D.F.A.
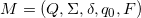 which recognises L.
which recognises L. - Construct a new D.F.A.
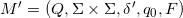 where the alphabet is the Cartesian product of the alphabet of M
with itself.
where the alphabet is the Cartesian product of the alphabet of M
with itself. - The transition function for
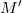 is
is 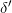 which is defined as follows:
which is defined as follows:
For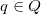 and
and 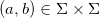 ,
,  .
. - Construct a new N.F.A.
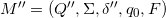 where
where 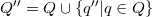 .
. - The transition function for
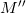 is
is 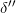 which is defined as follows:
which is defined as follows:
For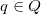 and
and 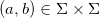 ,
, 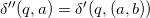 and
and 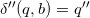 .
. 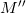 is the required N.F.A.
is the required N.F.A.
The D.F.A. 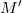 is constructed by taking pairs of symbols and leading to the state
where the automata would have reached if the symbols were provided
individually. The N.F.A.
is constructed by taking pairs of symbols and leading to the state
where the automata would have reached if the symbols were provided
individually. The N.F.A. 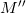 is constructed by adding dummy states corresponding to each state
where for individually processing the pair of symbols. The order of
processing is reversed. So, the N.F.A.
is constructed by adding dummy states corresponding to each state
where for individually processing the pair of symbols. The order of
processing is reversed. So, the N.F.A. 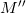 recognises the language swap_every_two(L) which makes it
a regular language.
recognises the language swap_every_two(L) which makes it
a regular language.
Not the answer you're looking for?
Similar Questions
Automata Theory and Formal Languages Instructions: Draw the DFA (Deterministic Finite Automaton) of the following: DFA...
3. (15 pt.) Prove that the class of regular languages is closed under intersection. That is,...
Each of the following languages is the union or intersection of two simpler languages. In each...
Let u and v be two particular strings over an alphabet Σ. Prove that the following...
Are the following languages over {a, b} regular? If they are then prove it. If they...
Provide direct answers. This question has been posted here by someone else before, but the answer...
Provide direct answers. This question has been posted here by someone else before, but the answer...
Let S denote the set of all possible finite binary strings, i.e. strings of finite length...
Automata Theory and Formal Languages Problems 1: Consider the following two grammars. Grammar G1- S →...
1. Given β = XT 1×nAn×nXn×1, show that the gradient of β with respect to X...
Need Online Homework Help?
Get Answers For Free
Most questions answered within 1 hours.
Active Questions
asked 33 minutes ago
asked 34 minutes ago
asked 43 minutes ago
asked 1 hour ago
asked 1 hour ago
asked 1 hour ago
asked 1 hour ago
asked 1 hour ago
asked 2 hours ago
asked 2 hours ago
asked 2 hours ago
asked 2 hours ago
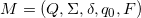 which recognises L.
which recognises L.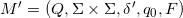 where the alphabet is the Cartesian product of the alphabet of M
with itself.
where the alphabet is the Cartesian product of the alphabet of M
with itself.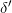 which is defined as follows:
which is defined as follows: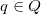 and
and 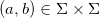 ,
,  .
.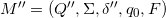 where
where 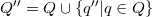 .
.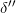 which is defined as follows:
which is defined as follows: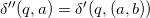 and
and 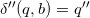 .
.