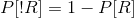You're about to get on a plane to Seattle. You want to know if you should...
You're about to get on a plane to Seattle. You want to know if you should bring an umbrella. You call 3 random friends of yours who live there and ask each independently if it's raining. Each of your friends has a 2/3 chance of telling you the truth and a 1/3 chance of messing with you by lying. All 3 friends tell you that "Yes" it is raining. What is the probability that it's actually raining in Seattle?
Homework Answers
We will start by considering the various events:
- Probability of rain in Seattle is

- Probability of not raining in
Seattle is
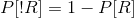
- Probability of all three friends
saying yes is
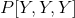
- Probability of all three friends
saying yes given it is actually raining is

- Probability of all three friends
saying yes given it is actually not raining is
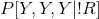
- Probability that it's actually
raining given all three friends said yes is
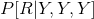 . This is the value we need to evaluate in our question.
. This is the value we need to evaluate in our question.
The first observation is that when all three friends say it is raining, it is either that all three are speaking truth or all three are lying. If it is actually raining, all three are speaking truth, else all three are lying.
Given that  and
and  . Thus
. Thus 

and
and 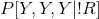

Now probability of all three saying yes is given by,



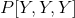

The formula for Baye's theorem is given by,

Using baye's formula, the probability that it's actually raining given all three friends said yes is given by,



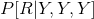

The probability that it's
actually raining given all three friends said yes
is 
SPECIFIC SCENARIOS:
1) Assume that the prior
probabilities of raining  :
:
Then probability of all three saying yes is given by,
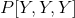


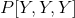

The probability that it's actually raining given all three friends said yes is given by,
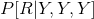


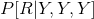

2) Assume that the prior
probabilities of raining  :
:
Then probability of all three saying yes is given by,
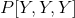


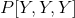

The probability that it's actually raining given all three friends said yes is given by,
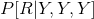


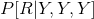

Not the answer you're looking for?
Similar Questions
Please read article, Business doesn't happen face to face as often as some would like. Instead,...
The assignment summary sheets will be submitted week 14 with Test 3. You are to personally...
As you saw from the lab PowerPoint slides last week, you will be doing a research...
In narrative essay format, I want you to address a business/organization case study using multiple concepts...
Ms Aaliyah Abimbola Background information for the assignment. You are the RN on a morning shift...
You are the RN on a morning shift on the respiratory ward of a large inner-city...
Background information for the assignment. You are the RN on a morning shift on the respiratory...
Please read the article and answear about questions. Determining the Value of the Business After you...
Powerpoint slides for COPD with the given case study by using CRC. Ms Aaliyah Abimbola Background...
Ms Aaliyah Abimbola; a 56-year old female who emigrated from Africa 20 years ago. Ms Abimbola...
Need Online Homework Help?
Get Answers For Free
Most questions answered within 1 hours.
Active Questions
asked 12 minutes ago
asked 13 minutes ago
asked 23 minutes ago
asked 36 minutes ago
asked 38 minutes ago
asked 38 minutes ago
asked 41 minutes ago
asked 44 minutes ago
asked 47 minutes ago
asked 51 minutes ago
asked 57 minutes ago
asked 1 hour ago